Расстояние от точки до прямой в пространстве.

Нравится

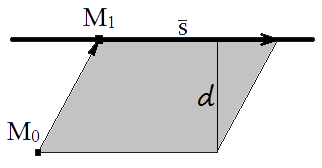
$Расстояние от точки до прямой$

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Если

;

- направляющий вектор прямой

, M₁(

₁,

₁) - точка лежащей на прямой, тогда расстояние от точки M₀(

₀,

₀) до прямой

можно найти, используя формулу

d =	\| M₀M₁ × s \|
	\| s \|

Вывод формулы
Если задано уравнение прямой

то несложно найти

;

- направляющий вектор прямой и M₁(

₁,

₁) - координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах

S = |

M₀M₁

С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне

S = |

В нашем случае высота будет равна расстоянию от точки до плоскости

, а сторона параллелограмма равна модулю направляющего вектора

.
Приравняв площади несложно получить формулу расстояния от точки до прямой.

Пример. Найти расстояние между точкой M(0, 2, 3) и прямой

x - 3	=	y - 1	=	z + 1
2	=	1	=	2

Решение.
Из уравнения прямой получим

{

2; 1; 2

}

- направляющий вектор прямой;
M₁(3; 1; -1) - точка лежащая на прямой.

Тогда

M₀M₁

{

3 - 0; 1 - 2; -1 - 3

}

{

3; -1; -4

}

M₀M₁ × s =	i	j	k	=
	3	-1	-4
	2	1	2

((-1)·2 - (-4)·1) -

(3·2 - (-4)·2) +

(3·1 -(-1)·2) =

{

2; -14; 5

}

d =	\| M₀M₁ × s \|	=	(2² + (-14)² + 5²)^1/2	=	225^1/2	= 5
	\| s \|		(2² + 1² + 2²)^1/2		9^1/2

Ответ: расстояние от точки до прямой равно 5.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты.

Аналитическая геометрия: Вступление и оглавление.

Нравится

Добавить комментарий