 | Математический образовательный портал. "Математика это просто!" - посетите наш сайт и убедитесь в этом. |
- Калькуляторы
- Справочник
Расстояние между плоскостями.
| Twitt | Нравится |
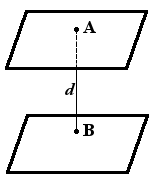
Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.
Если заданы уравнения параллельных плоскостей A
x
+ By
+ Cz
+ D1 = 0 и Ax
+ By
+ Cz
+ D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулуd = |
|D2 - D1| |
| √ A2 + B2 + C2 |
Смотрите также: Онлайн калькулятор. Расстояние между плоскостями.
Пример. Найти расстояние между плоскостями 2
x
+ 4y
- 4z
- 6 = 0 и x
+ 2y
- 2z
+ 9 = 0.
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2x
+ 4y
- 4z
+ 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
d = |
|18 - (-6)| | = | |24| | = | 24 | = 4 |
| √ 22 + 42 + (-4)2 |
√ 36 |
6 |
Ответ: расстояние между плоскостями равно 4.
Аналитическая геометрия: Вступление и оглавление.
- Расстояние между двумя точками.
- Середина отрезка. Координаты середины отрезка.
- Уравнение прямой.
- Расстояние от точки до прямой на плоскости.
- Расстояние от точки до прямой в пространстве.
- Уравнение плоскости.
- Расстояние от точки до плоскости.
- Расстояние между плоскостями.
- Угол между прямой и плоскостью.
- Угол между плоскостями.
| Twitt | Нравится |
Добавить комментарий
© 2013-2026 Довжик Михаил Копирование материала запрещено. |
СЕРВИСЫ Онлайн калькуляторы Справочник Таблицы и формулы |
O-Math.com О проекте Помочь сайту support@o-math.com |